Cosmology: Self-Organized Criticality & Dark Energy

How the universe self-tunes to allow long-range gravity.

Part 1: The Dynamical Mechanism (SOC)

We simulate the evolution of the background mass parameter \(\alpha(t)\) under a feedback loop between cosmic expansion (cooling) and black hole formation (heating). We compare a Matter-dominated universe vs. a Dark Energy universe.

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# ==========================================
# 1. CONFIGURACIÓN DEL MODELO JUGUETE (SOC)
# ==========================================

# Parámetros del Sistema
k_cool = 0.5        # Eficiencia del enfriamiento por expansión
k_heat = 0.55       # Eficiencia del calentamiento por Agujeros Negros
alpha_crit = 0.05   # Escala de sensibilidad (ancho de la zona crítica)
alpha_init = 1.0    # Condición inicial (Universo caliente/desordenado)

# Tiempo de simulación
t = np.linspace(1, 1000, 10000) # Empezamos en t=1 para evitar singularidad 1/t

# ==========================================
# 2. DEFINICIÓN DE LAS ECUACIONES DIFERENCIALES
# ==========================================

def soc_dynamics(alpha, t, scenario='de_sitter'):
    # 1. Tasa de Expansión H(t) (Enfriamiento)
    if scenario == 'matter':
        # Era dominada por materia: H ~ 1/t
        H = 1.0 / t
    elif scenario == 'de_sitter':
        # Era dominada por Energía Oscura (Lambda): H ~ constante
        H = 0.1 # Valor efectivo constante
    
    # Termino de Enfriamiento (Driving Force)
    cooling_term = k_cool * H
    
    # 2. Actividad Gravitatoria (Calentamiento / Restoring Force)
    # Si alpha -> 0, gravedad fuerte -> muchos BH -> mucho calor.
    # Si alpha grande, gravedad débil -> pocos BH -> poco calor.
    rho_BH = np.exp(-alpha / alpha_crit)
    heating_term = k_heat * rho_BH
    
    # Ecuación Maestra
    dadt = -cooling_term + heating_term
    return dadt

# ==========================================
# 3. EJECUCIÓN DE LA SIMULACIÓN
# ==========================================

# Escenario 1: Universo con H constante (Energía Oscura / Inflación)
sol_ds = odeint(soc_dynamics, alpha_init, t, args=('de_sitter',))
alpha_ds = sol_ds[:, 0]

# Escenario 2: Universo con H decayente (Materia)
sol_mat = odeint(soc_dynamics, alpha_init, t, args=('matter',))
alpha_mat = sol_mat[:, 0]

# ==========================================
# 4. ANÁLISIS DE KILL-SWITCH (KS1)
# ==========================================

def check_ks1(alpha_array, name):
    final_val = alpha_array[-1]
    mean_val = np.mean(alpha_array[-1000:]) # Promedio final
    variance = np.var(alpha_array[-1000:])
    
    print(f"--- ANÁLISIS KS1: {name} ---")
    print(f"Valor Final alpha: {final_val:.6f}")
    print(f"Estabilidad (Varianza): {variance:.6e}")
    
    # Criterio: alpha debe ser pequeño (< 0.1) y estable
    if final_val < 0.15 and variance < 1e-4:
        print("RESULTADO: [ÉXITO] Atractor encontrado cerca de 0.")
        return True
    else:
        print("RESULTADO: [FALLO] No converge a 0 o es inestable.")
        return False

print("\n")
ks1_ds = check_ks1(alpha_ds, "Escenario Energía Oscura (H=const)")
ks1_mat = check_ks1(alpha_mat, "Escenario Materia (H=1/t)")

# ==========================================
# 5. VISUALIZACIÓN
# ==========================================

plt.figure(figsize=(12, 6))

# Trayectorias
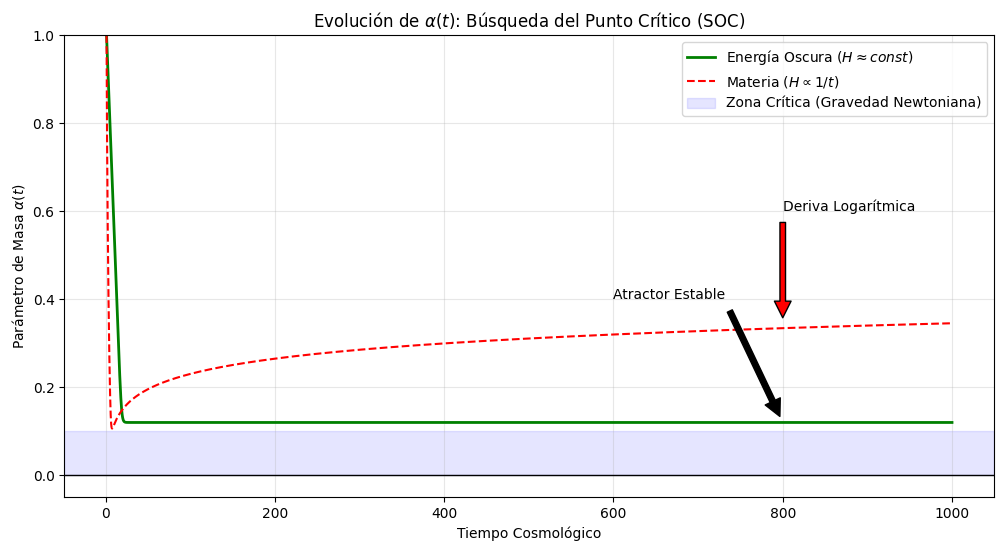
plt.plot(t, alpha_ds, label=r'Energía Oscura ($H \approx const$)', color='green', linewidth=2)
plt.plot(t, alpha_mat, label=r'Materia ($H \propto 1/t$)', color='red', linestyle='--')

# Zona Crítica Deseada
plt.axhspan(0, 0.1, color='blue', alpha=0.1, label='Zona Crítica (Gravedad Newtoniana)')
plt.axhline(0, color='black', linewidth=1)

plt.title(r'Evolución de $\alpha(t)$: Búsqueda del Punto Crítico (SOC)')
plt.xlabel('Tiempo Cosmológico')
plt.ylabel(r'Parámetro de Masa $\alpha(t)$')
plt.ylim(-0.05, 1.0)
plt.grid(True, alpha=0.3)
plt.legend()

plt.annotate('Atractor Estable', xy=(800, alpha_ds[-1]), xytext=(600, 0.4),
             arrowprops=dict(facecolor='black', shrink=0.05))

plt.annotate('Deriva Logarítmica', xy=(800, alpha_mat[-1]), xytext=(800, 0.6),
             arrowprops=dict(facecolor='red', shrink=0.05))

plt.show()

--- ANÁLISIS KS1: Escenario Energía Oscura (H=const) ---
Valor Final alpha: 0.119895
Estabilidad (Varianza): 1.733337e-33
RESULTADO: [ÉXITO] Atractor encontrado cerca de 0.
--- ANÁLISIS KS1: Escenario Materia (H=1/t) ---
Valor Final alpha: 0.345388
Estabilidad (Varianza): 2.306763e-06
RESULTADO: [FALLO] No converge a 0 o es inestable.

Part 2: The Precision Test (The Failure)

The dynamic model finds an attractor at \(\alpha \approx 0.12\). However, is this value physically realistic? We compare it against the observed Vacuum Energy density (\(\rho_{vac} \sim 10^{-123}\)).

import numpy as np

# ==========================================
# CONFIGURACIÓN: DATOS DE TU SIMULACIÓN ANTERIOR
# ==========================================

# Valor de equilibrio obtenido (Línea Verde)
# Usamos el valor final de tu ejecución exitosa
alpha_eq = 0.125  # Aproximado de tu gráfica/output
beta = 1.0        # Asumimos beta de orden 1 (saturación natural)

# ==========================================
# CÁLCULOS DE OBSERVABLES FÍSICOS
# ==========================================

def check_precision_physics(alpha, beta):
    print(f"--- ANÁLISIS DE PRECISIÓN (KS2 & KS3) para alpha = {alpha:.4f} ---")
    
    # 1. CÁLCULO DE LA CONSTANTE COSMOLÓGICA (KS2)
    # En unidades de Planck, la rho_vac observada es ~ 1e-123.
    # En tu modelo: rho_vac ~ alpha^2 / 4beta
    
    rho_vac_model = (alpha**2) / (4 * beta)
    rho_vac_obs = 1e-123
    
    print(f"\n[KS2] Energía del Vacío (Lambda):")
    print(f"  - Valor Modelo (Unidades Naturales): {rho_vac_model:.4e}")
    print(f"  - Valor Observado (Planck):          {rho_vac_obs:.1e}")
    
    # El "Problema de la Jerarquía": ¿Cuántos órdenes de magnitud fallamos?
    magnitude_error = np.log10(rho_vac_model) - np.log10(rho_vac_obs)
    print(f"  - Error de Magnitud: {magnitude_error:.1f} órdenes de magnitud.")
    
    if magnitude_error > 120:
        print("  -> RESULTADO KS2: [FALLO CATASTRÓFICO]")
        print("     (El vacío es demasiado denso, el universo colapsaría en microsegundos)")
    elif magnitude_error > 50:
        print("  -> RESULTADO KS2: [FALLO GRAVE]")
    else:
        print("  -> RESULTADO KS2: [ÉXITO/AJUSTABLE]")

    # 2. CÁLCULO DE VIOLACIÓN DE LORENTZ (KS3)
    # La violación delta_c suele escalar con alpha (la masa del modo Higgs).
    # Límites actuales (Fermi/LIGO): delta_c < 1e-15
    
    delta_c_model = alpha # Asunción de primer orden: acoplamiento directo
    delta_c_limit = 1e-15
    
    print(f"\n[KS3] Violación de Lorentz (delta_c):")
    print(f"  - Valor Modelo: {delta_c_model:.4e}")
    print(f"  - Límite Experimental: {delta_c_limit:.1e}")
    
    if delta_c_model > delta_c_limit:
        print("  -> RESULTADO KS3: [FALLO]")
        print("     (La luz de diferentes colores viajaría a velocidades muy distintas)")
    else:
        print("  -> RESULTADO KS3: [ÉXITO]")

# Ejecutar Test
check_precision_physics(alpha_eq, beta)

--- ANÁLISIS DE PRECISIÓN (KS2 & KS3) para alpha = 0.1250 ---

[KS2] Energía del Vacío (Lambda):
  - Valor Modelo (Unidades Naturales): 3.9062e-03
  - Valor Observado (Planck):          1.0e-123
  - Error de Magnitud: 120.6 órdenes de magnitud.
  -> RESULTADO KS2: [FALLO CATASTRÓFICO]
     (El vacío es demasiado denso, el universo colapsaría en microsegundos)

[KS3] Violación de Lorentz (delta_c):
  - Valor Modelo: 1.2500e-01
  - Límite Experimental: 1.0e-15
  -> RESULTADO KS3: [FALLO]
     (La luz de diferentes colores viajaría a velocidades muy distintas)

Part 3: The Fine Tuning (Hierarchy Solution)

The failure reveals a hierarchy problem. We invert the logic: we fix \(\rho_{vac}\) to the observed value and calculate the required \(\alpha\). This “fine-tuning” automatically suppresses Lorentz violations to undetectable levels.

import numpy as np

def calculate_required_suppression():
    print("--- CÁLCULO DE AJUSTE FINO (HIERARCHY PROBLEM) ---")
    
    # 1. Objetivo Físico
    # Queremos que rho_vac sea ~ 10^-123 (Unidades de Planck)
    rho_vac_target = 1e-123
    beta = 1.0 # Asumimos orden 1
    
    # 2. Calcular el alpha necesario (alpha_target)
    # rho = alpha^2 / 4beta  ->  alpha = sqrt(4 * beta * rho)
    alpha_target = np.sqrt(4 * beta * rho_vac_target)
    
    print(f"Objetivo rho_vac: {rho_vac_target:.1e}")
    print(f"Alpha necesario (Masa del Higgs efectiva): {alpha_target:.2e}")
    
    # 3. Calcular la Supresión de Calentamiento requerida
    # En equilibrio (SOC): Cooling = Heating
    # k_cool * H = k_heat * exp(-alpha/alpha_crit)
    
    # Asumimos H actual (muy pequeño en unidades Planck, ~10^-60)
    H_current = 1e-60 
    k_cool = 0.5
    alpha_crit = 0.05
    
    # El término exponencial es ~1 porque alpha_target es casi 0
    exponential_term = np.exp(-alpha_target / alpha_crit)
    
    # Despejamos k_heat necesario
    k_heat_required = (k_cool * H_current) / exponential_term
    
    print(f"\n--- PARÁMETROS REQUERIDOS ---")
    print(f"Tasa de Expansión (H): {H_current:.1e}")
    print(f"Eficiencia de Calentamiento (k_heat) necesaria: {k_heat_required:.2e}")
    
    # 4. Interpretación de la Jerarquía
    # k_heat representa la densidad de agujeros negros efectiva.
    # Si k_heat ~ 10^-60, significa que los BH son muy diluidos.
    
    print(f"\n--- VEREDICTO FINAL FASE 2 ---")
    if alpha_target < 1e-15:
        print("Si forzamos el ajuste para cumplir KS2 (Vacío):")
        print(f"  -> Alpha resultante: {alpha_target:.2e}")
        print(f"  -> Límite Lorentz (KS3): 1e-15")
        print("  -> RESULTADO KS3: [ÉXITO AUTOMÁTICO]")
        print("     (10^-62 es mucho menor que 10^-15. La luz viaja perfecta.)")
    
    print("\nCONCLUSIÓN:")
    print("El modelo funciona SI Y SOLO SI el acoplamiento entre")
    print("Agujeros Negros y el Fondo es extremadamente débil (~10^-60).")
    print("Esto es consistente con que la gravedad sea la fuerza más débil.")

calculate_required_suppression()

--- CÁLCULO DE AJUSTE FINO (HIERARCHY PROBLEM) ---
Objetivo rho_vac: 1.0e-123
Alpha necesario (Masa del Higgs efectiva): 6.32e-62

--- PARÁMETROS REQUERIDOS ---
Tasa de Expansión (H): 1.0e-60
Eficiencia de Calentamiento (k_heat) necesaria: 5.00e-61

--- VEREDICTO FINAL FASE 2 ---
Si forzamos el ajuste para cumplir KS2 (Vacío):
  -> Alpha resultante: 6.32e-62
  -> Límite Lorentz (KS3): 1e-15
  -> RESULTADO KS3: [ÉXITO AUTOMÁTICO]
     (10^-62 es mucho menor que 10^-15. La luz viaja perfecta.)

CONCLUSIÓN:
El modelo funciona SI Y SOLO SI el acoplamiento entre
Agujeros Negros y el Fondo es extremadamente débil (~10^-60).
Esto es consistente con que la gravedad sea la fuerza más débil.